Vous aimez bien les diagrammes en barres ? Vous voulez montrer graphiquement la différence de mesures entre deux groupes ? J’ai ce qu’il vous faut: le bar-bar-plot !

Mon premier bar-bar-plot

Créons d’abord un petit jeu de données, bien propre, comme on vous a déjà expliqué dans « Les dix commandements d’une base de données réussie« . Ici nous aurons la taille des individus de deux groupes différents, un peu d’aléatoire et des lois Gaussiennes. Parce qu’on aime bien les lois Gaussiennes en statistiques.

library(tibble)
set.seed(4321)
data <- tibble(
  Taille = c(rnorm(40, 170, 30), rnorm(25, 145, 10), rnorm(25, 195, 10)),
  Groupe = c(rep("A", 40), rep("B", 50))
)

Et comme on a envie de savoir si nos deux groupes ont en moyenne la même taille, rien de tel qu’un joli bar-bar-plot.

library(dplyr)
library(ggplot2)
info <- data %>%
  group_by(Groupe) %>%
  summarise(Moyenne = mean(Taille),
            Ecart = sd(Taille))
ggplot(info, aes(x = Groupe, y = Moyenne, fill = Groupe)) +
  geom_bar(stat = "identity", position = position_dodge(),
           colour = "grey30") +
  geom_errorbar(
    aes(ymin = Moyenne - Ecart, ymax = Moyenne + Ecart),
    width = .2, position = position_dodge(.9), size = 1
  ) + 
  scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  scale_fill_viridis_d() +
  guides(fill = FALSE)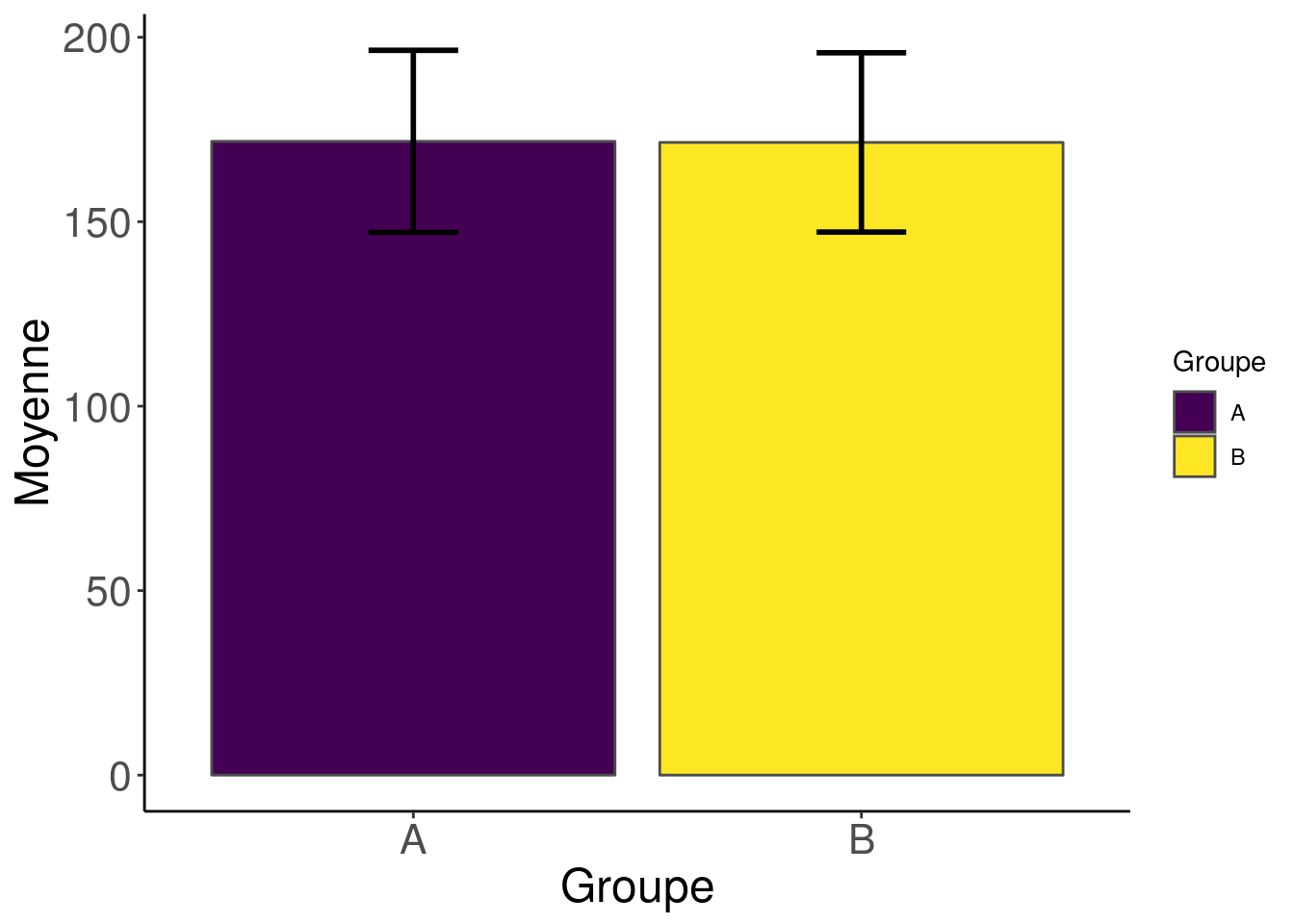

Parfait ! Nos deux groupes ont la même moyenne ! En plus, les barres d’erreurs se recouvrent donc le test va nous dire qu’il n’y a pas de différence statistique entre les deux groupes !

STOP ! Vous êtes sûrs de ce que vous faîtes là ? Vous devriez retourner lire notre article sur “Les pièges de la représentation des données”. Nous vous avons déjà dit que le bar-bar-plot était à bannir. Il ne représente pas vos données et il induit en erreur.

Par ailleurs, attention, la différence statistique entre les moyennes de deux groupes ne se regarde pas en comparant les écart-types des distributions. Elle se peut se représenter au travers de l’intervalle de confiance de l’estimation de la moyenne. Du coup, la soit-disant barre d’erreur n’est en aucun cas un moyen visuel de représenter le résultat d’un éventuel test statistique de comparaison de moyenne. Et si jamais vous calculez l’écart-type de la distribution de l’estimation de la moyenne, vous devriez afficher une barre d’environ 2 fois l’écart-type de chaque côté de la moyenne pour une représentation de l’intervalle de confiance à 95%.

Mais alors ? Comment je fais une belle représentation de mes données pour mettre en évidence la réponse à la question que je me pose, sans qu’aucun lecteur ne remette en question mon intégrité ?

Les représentations recommandées

Le diagramme en barres pour comparer les comptages

Afficher des données sous forme de barres implique que la surface de ces barres représente une quantité que l’on pourrait voir directement dans la vraie vie. Vous devez imaginez que vous prenez une photo de profil de grands sacs à patates dans lesquels vous avez mis les objets que vous voulez quantifier. Si ce n’est pas possible de le faire en vrai, alors le diagramme en barres n’est pas adapté.

Ici, nous pouvons comparer le nombre d’individus dans chaque groupe par exemple. Parce qu’il est possible de mettre tous les individus dans deux gros sacs.

C’est aussi une bonne manière de nous rappeler qu’on n’a pas du tout évoqué ce nombre d’individus dans notre mauvais bar-bar-plot de comparaison de moyennes. Pourtant, c’est important les effectifs dans les tests statistiques, non ?

ggplot(data) + 
  geom_bar(aes(Groupe, fill = Groupe)) + 
  scale_fill_viridis_d() +
  scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  guides(fill = FALSE)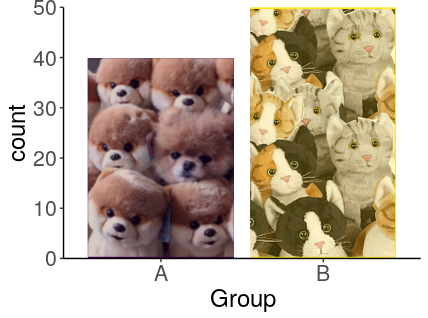

Oui, on a un peu triché pour ce dernier, mais c’est pour la représentation sac à patates…

L’histogramme pour comparer les données continues

On ne peut pas mettre des valeurs de tailles d’individus dans un sac à patate, par contre, on peut mettre tous les individus de la même taille dans un même sac. D’où les barres de l’histogramme.

ggplot(data) + 
  geom_histogram(aes(Taille, fill = Groupe),
                 position = "identity",
                 alpha = 0.60,
                 bins = 10) +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0))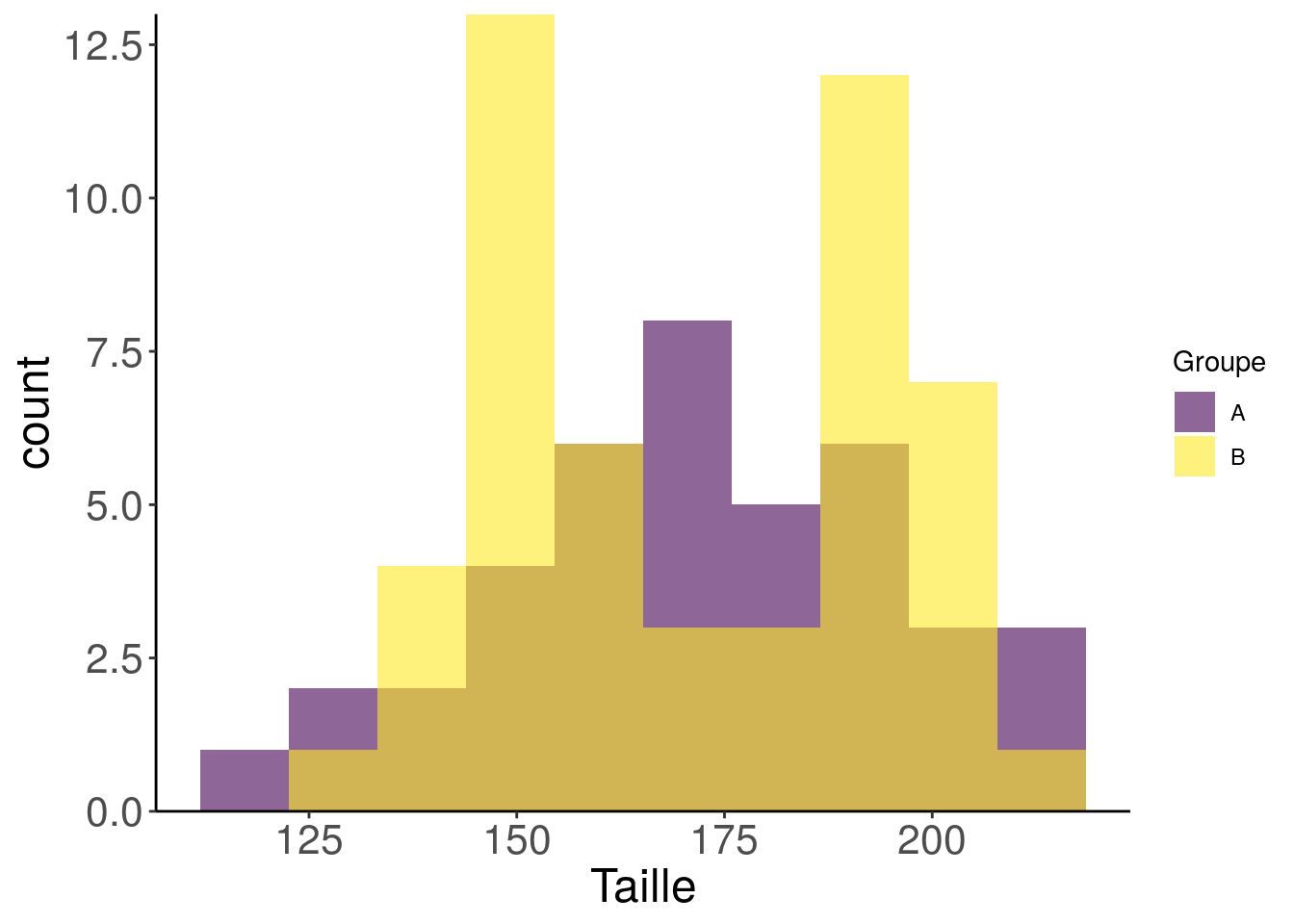

Avouons que pour un graphique final, l’histogramme n’est pas la plus élégante des représentations. Nous pourrions commencer par le lisser un peu avec geom_density. Le degré de lissage ça se choisit, c’est comme le nombre de classes pour un histogramme.

ggplot(data) + 
  geom_density(aes(Taille, fill = Groupe), 
                 position = "identity",
                 alpha = 0.60) +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0))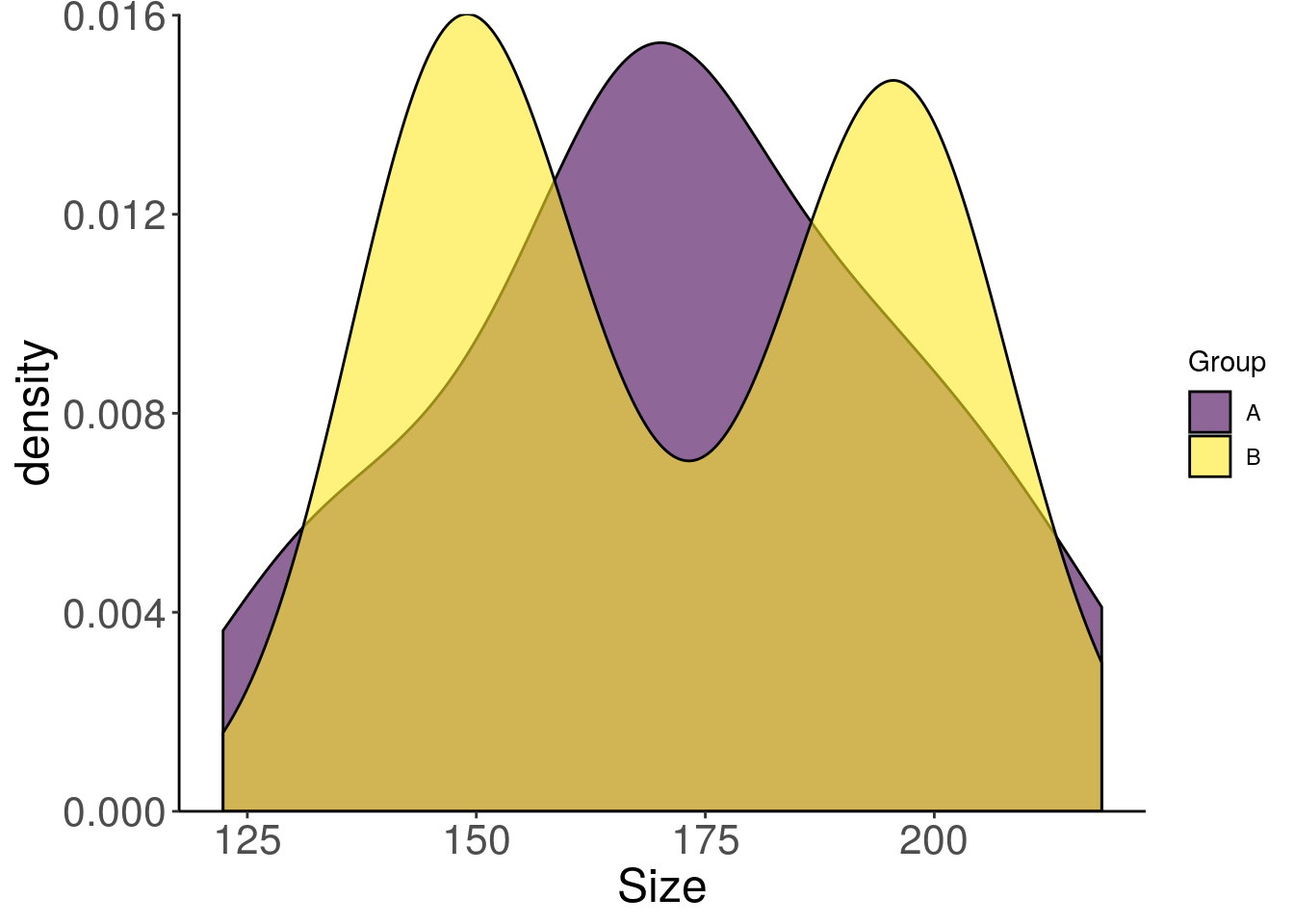

Le violin plot pour mieux comparer

Nous pouvons afficher les densités de distribution précédentes de manière verticale pour retrouver un graphique que l’on visualise mieux. Avec la médiane en bonus.

ggplot(data) + 
  geom_violin(aes(Groupe, Taille, fill = Groupe), 
                 position = "identity",
              draw_quantiles = c(0.5),
              colour = "grey30") +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
   guides(fill = FALSE)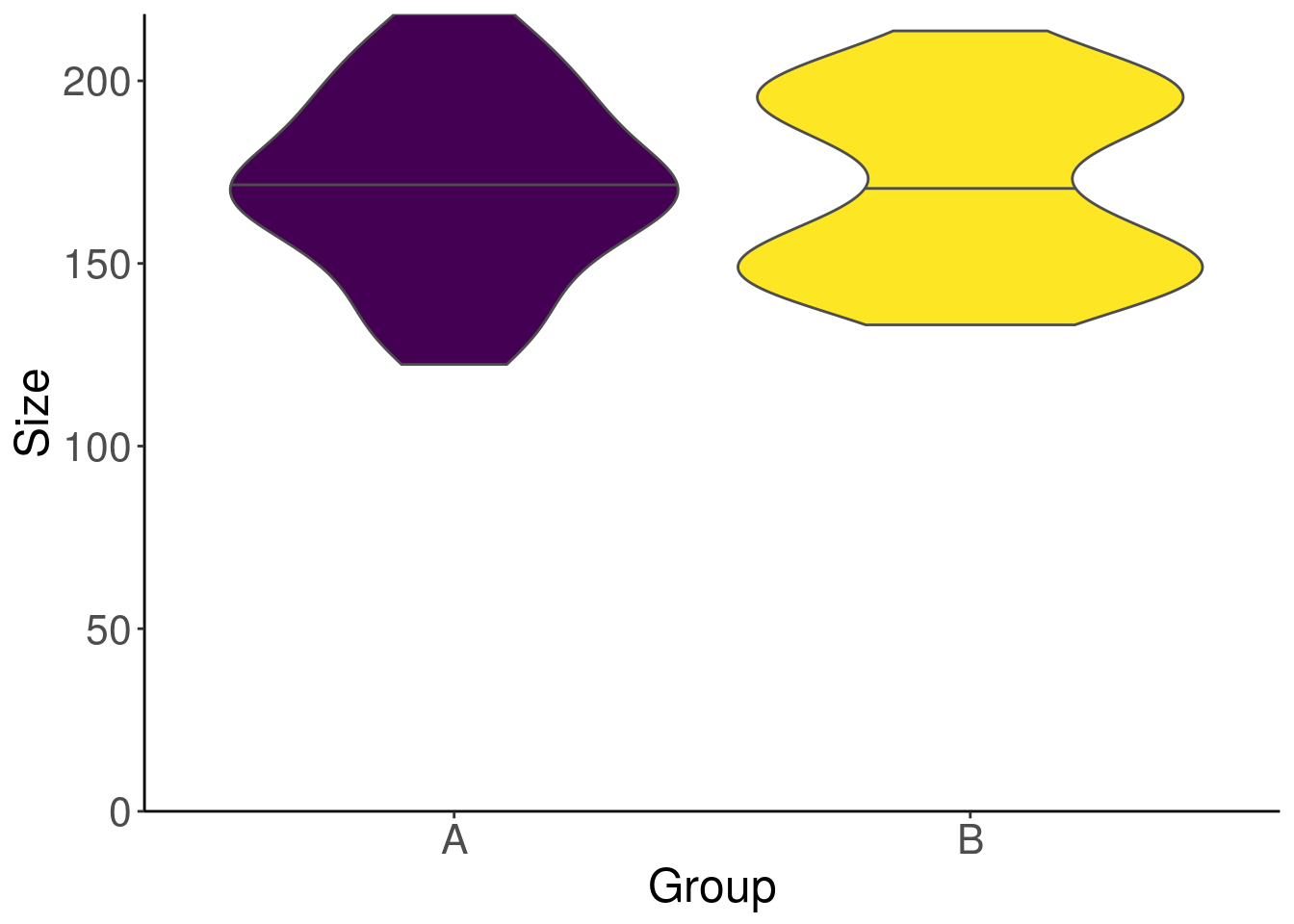

On ne peut plus cacher l’aspect bimodal du Groupe B. Toutefois, on n’a pas d’idée du nombre d’individus utilisé pour réaliser cette figure. On ne voudrait pas mentir à nos lecteurs…?
Par ailleurs, si vous avez peu d’individus dans chaque groupe, le violin plot ne rend pas toujours très bien. Vous pouvez choisir de ne garder que le geom_dotplot avec un binwidth adapté à vos données. C’est un choix.

library(cowplot)
# sample size
sample_size <- data %>% count(Groupe)
data_size <- data %>% 
  left_join(sample_size, by = "Groupe") %>% 
  mutate(myaxis = paste0(Groupe, "\n", "n=", n))
# violin with median
g1 <- ggplot(data_size) + 
  aes(myaxis, Taille, fill = Groupe) +
  geom_violin(position = "identity",
              draw_quantiles = c(0.5),
              colour = "grey10", alpha = 0.7,
              scale = "count") +
    geom_dotplot(method = "histodot", binaxis = "y",
                 dotsize = 0.8, binwidth = 10,
                 stackdir = "center"
                 ) +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                       expand = c(0, 0)) +
  xlab(NULL) +
  guides(fill = FALSE)
# dotplot with mean
g2 <- ggplot(data_size) + 
  aes(myaxis, Taille, fill = Groupe) +
    geom_dotplot(method = "histodot", binaxis = "y",
                 dotsize = 1, binwidth = 10,
                 stackdir = "center"
                 ) +
  stat_summary(fun.y = "mean", fun.ymin = "mean", fun.ymax = "mean", size = 0.5,
               geom = "crossbar", colour = "grey30") +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                       expand = c(0, 0)) +
  xlab(NULL) +
  guides(fill = FALSE)
cowplot::plot_grid(plotlist = list(g1, g2))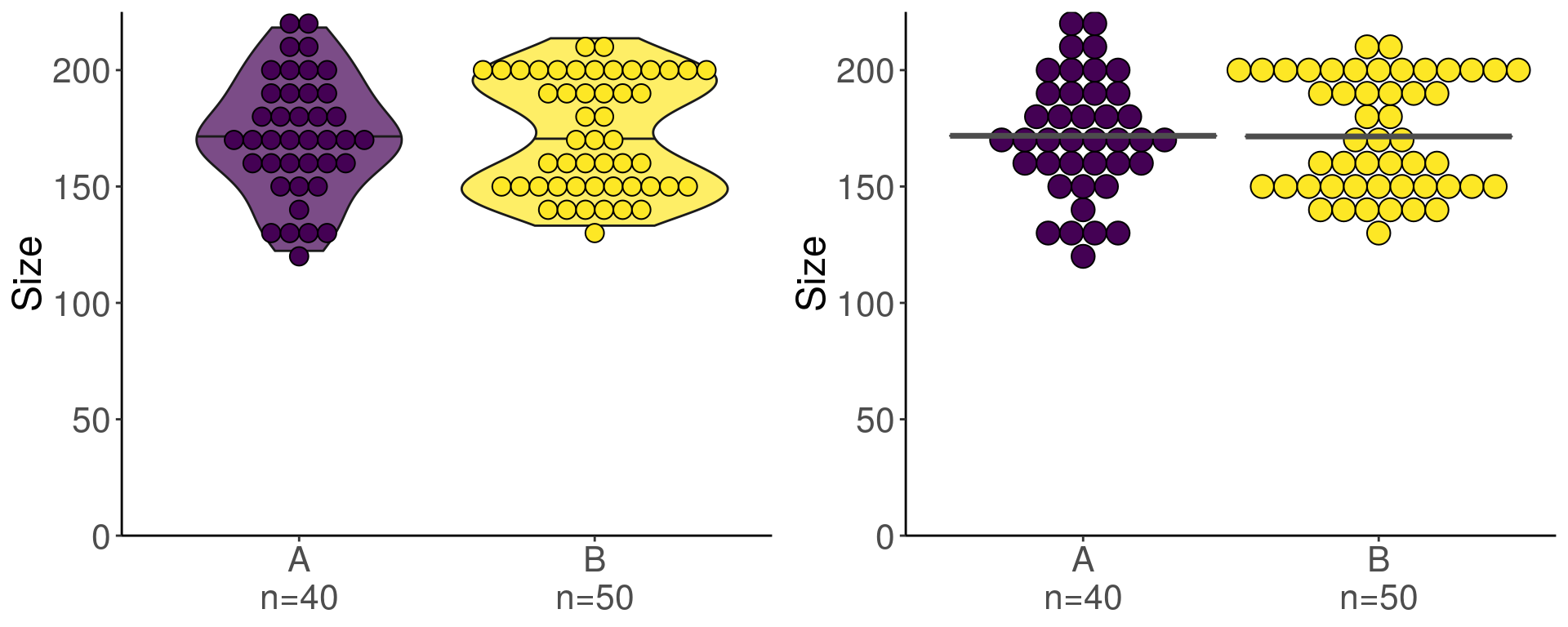

Avec ce genre de données, on sait qu’on ne peut pas aller plus loin dans l’analyse statistique sans violer les hypothèses de construction de certains tests…

Au final, pensez à choisir des représentations qui ne laisserons pas de doutes sur votre honnêteté intellectuelle. Le site data-to-viz.com peut vous y aider.

Pour information, nous avons défini un thème par défaut pour cet article theme_set(theme_classic())